Lightsail의 WordPress 인스턴스를 AL2023으로 전환 할 때, All-in-One Migration utility로 import를 시도하는데 이전에 본 적이 없던 internal error가 발생했다. 분명 업로드 가능한 파일 크기도 import하는 압축 파일 보다 크게 설정해 주었고 다른 설정들도 모두 마쳤음에도 계속해서 실패하는 것이다.
YYYY/MM/DD HH:MM:SS [error] 32777#32777: *4 FastCGI sent in stderr: "PHP message: PHP Fatal error: Uncaught ValueError: Path cannot be empty in /var/www/html/wp-content/plugins/all-in-one-wp-migration/functions.php:1881
Stack trace:
#0 /var/www/html/wp-content/plugins/all-in-one-wp-migration/functions.php(1881): fopen()
#1 /var/www/html/wp-content/plugins/all-in-one-wp-migration/lib/model/import/class-ai1wm-import-upload.php(86): ai1wm_is_filedata_supported()
#2 /var/www/html/wp-content/plugins/all-in-one-wp-migration/lib/controller/class-ai1wm-import-controller.php(77): Ai1wm_Import_Upload::execute()
#3 /var/www/html/wp-includes/class-wp-hook.php(341): Ai1wm_Import_Controller::import()
#4 /var/www/html/wp-includes/class-wp-hook.php(365): WP_Hook->apply_filters()
#5 /var/www/html/wp-includes/plugin.php(522): WP_Hook->do_action()
#6 /var/www/html/wp-admin/admin-ajax.php(192): do_action()
#7 {main}
thrown in /var/www/html/wp-content/plugins/all-in-one-wp-migration/functions.php on line 1881" while reading response header from upstream, client: [CLIENT_IP], server: _, request: "POST /wp-admin/admin-ajax.php?action=ai1wm_import&ai1wm_import=1 HTTP/1.1", upstream: "fastcgi://unix:/run/php-fpm/www.sock:", host: "[SERVER_IP]", referrer: "http://[SERVER_IP]/wp-admin/admin.php?page=ai1wm_import"
메모리 문젠가?
Nginx의 로그를 보니 Path cannot be empty ... 라는 PHP Fatal error가 찍혀 있었다. 이 에러메세지 자체로는 문제점이 잘 드러나지 않지만, 검색해보니 업로드가 완료된 후 압축 해제와 import를 처리 하는 과정중에 메모리가 부족해서 이런 문제가 발생할 수 있다는 내용이 있었는데, 업로드가 100%까지 진행되고 나서 그 후에 문제가 발생하는 것으로 볼 때 이 말이 사실일 가능성이 있어 보였다.
혹시나 해서 지금 사용하고 있는 것보다 높은 사양의 인스턴스를 하나 새로 파서 테스트해 보니 오류없이 잘 동작했다. 여기까지 확인해서 메모리 부족 때문에 발생하는 문제라는 확증이 들자 한가지 꼼수가 떠올랐다.
- 높은 사양의 인스턴스로 All-in-One으로 마이그레이션을 하고
- 스냅샷을 하나 만든 다음
- 스냅샷으로 부터 원래의 낮은 사양으로 인스턴스를 생성한다.
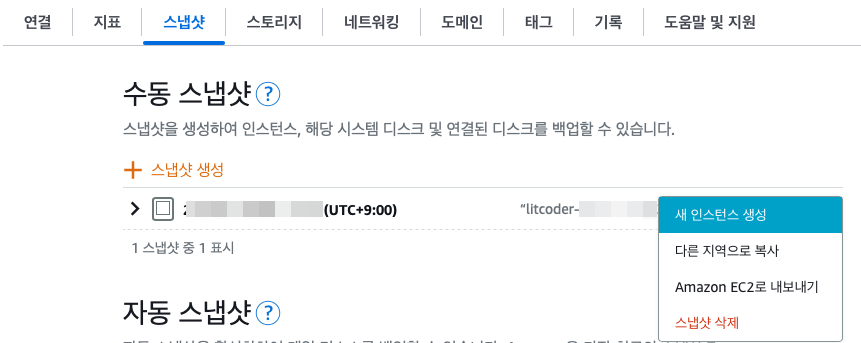
“그래, 이런 기발한 방법이!” 라며 먼저 $12짜리 인스턴스에 마이그레이션을 완료하고 스냅샷을 만들었다. 그리고 나서 스냅샷으로 부터 인스턴스를 생성하려고 하는데 이런화면이 나왔다.

스냅샷을 생성할 때의 인스턴스보다 낮은 티어는 생성할 수가 없다는 것이다.
결론
